MATEMATIKA




je souhrn určitých objektů, tyto objekty nazýváme prvky množiny.
Množina může být určena:
- výčtem prvků
- uvedením charakteristické vlastnosti
Podmnožina
Množina
je podmnožinou množiny
právě tehdy, když každý prvek množiny
je zároveň prvkem množiny .
Zapisujeme:
.
Množiny se rovnají právě tehdy, když každý prvek množiny je prvkem množiny a obráceně.
Zapisujeme
.
Doplněk množiny v množině je množina všech prvků z , které nepatří do .
Zapisujeme
.
Průnik množin
- Je množina všech prvků, které patří zároveň do obou množin.
Sjednocení množin
- Je množina všech prvků, které patří aspoň do jedné z množin
.
Rozdíl množin
- Je množina všech prvků množiny
, které nejsou prvky množiny
.
- jsou množiny reálných čísel, které lze na číselné ose zobrazit úsečkou, polopřímkou nebo přímkou.
Uzavřený interval:

Interval zleva otevřený a zprava uzavřený:

Interval zleva uzavřený a zprava otevřený:

Otevřený interval:

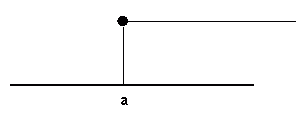
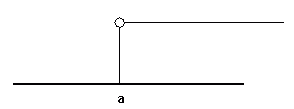
Intervaly neomezené zprava:
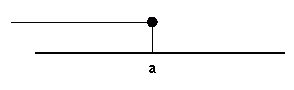
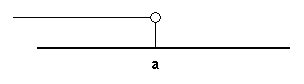
Intervaly neomezené zleva:
© 2010-2011 Petr Bělaška
